Table des matières

2. Méthode des matrices de transfert classique (en série)

3. Méthode des matrices de transfert en parallèle

1. Introduction

La méthode de matrice de transfert (TMM) est utilisée classiquement pour prédire des propriétés acoustiques des couches homogènes latéralement infinie assemblées en série pour former un empilement. Dans ce travail, un processus de montage en parallèle de matrices de transfert est mis en place afin de modéliser des matériaux hétérogènes tels que des patchworks, des mosaïques acoustiques, ou une collection d’éléments acoustiques en parallèle. La matrice de transfert résultante de l’ensemble parallèle est également une matrice 2 par 2 qui peuvent être assemblés en série avec la TMM classique. Dans ce document, il sera question de présenter les deux méthodes.

2. Méthode des matrices de transfert classique (en série)

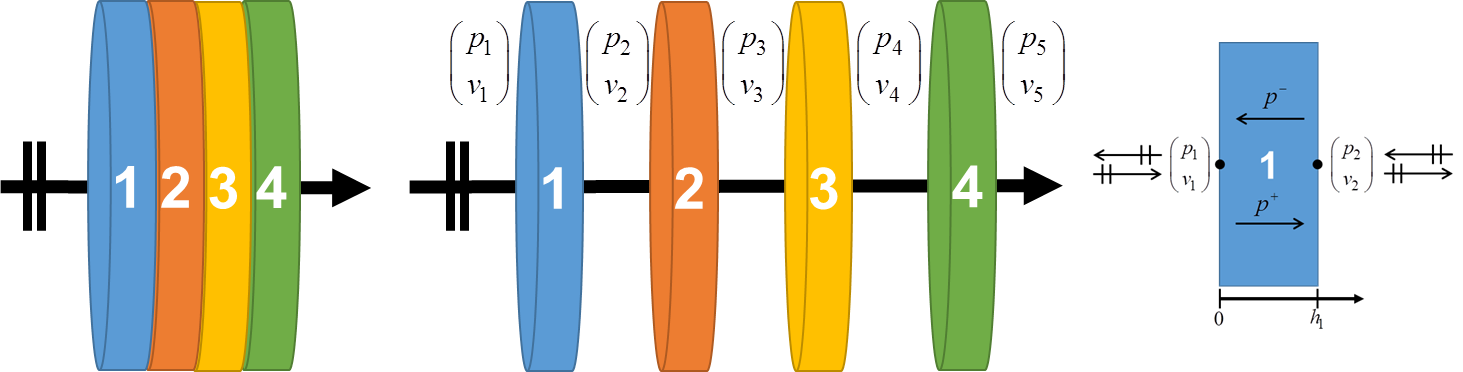
Figure 1. Schéma d’un empilement de 4 couches de matériaux

Afin d’explique la méthode des matrices de transfert classique, un exemple d’un empilement de quatre matériaux est présenté à la Figure 1. Cette méthode est dite « en série » dans la mesure où chaque matériaux est mis l’un derrière l’autre vis-à-vis de la propagation de l’onde sonore. Chaque couche est exprimée par une matrice 2 par 2 reliant la pression et la vitesse de part et d’autre de celle-ci. Afin de simplifier l’expression de cette matrice, chaque couche est considérée comme un fluide équivalent avec une impédance caractéristique $Z_i$ et un nombre d’onde $k_i$ . Ces deux propriétés sont données par des modèles (e.g. modèle de Miki, modèle de Johnson Champoux Allard) . En supposant qu’il n y a que des ondes planes qui se propagent dans la couche d’épaisseur $h_i$ , l’expression de la matrice de transfert est donnée par l’équation 1.

(1) $\begin{equation*}\begin{pmatrix}p_1\\v_1\end{pmatrix}=\begin{bmatrix} cos(k_1h_1) & jZ_1sin(k_1h_1) \\ j\frac{1}{Z_1}sin(k_1h_1) & cos(k_1h_1) \end{bmatrix}\begin{pmatrix}p_2\\v_2\end{pmatrix}=T_1\begin{pmatrix}p_2\\v_2\end{pmatrix}\end{equation*}$

En faisant la continuité de la pression et de la vitesse entre chaque couche, une matrice globale $T_G$ peut être déduite. L’équation 2 fournit les infos nécessaires au calcul de cette matrice.

(2) $\begin{equation*}\left.\begin{matrix}\begin{pmatrix}p_1\\v_1\end{pmatrix}=T_1\begin{pmatrix}p_2\\v_2\end{pmatrix}\\\begin{pmatrix}p_2\\v_2\end{pmatrix}=T_2\begin{pmatrix}p_3\\v_3\end{pmatrix}\\\begin{pmatrix}p_3\\v_3\end{pmatrix}=T_3\begin{pmatrix}p_4\\v_4\end{pmatrix}\\\begin{pmatrix}p_4\\v_4\end{pmatrix}=T_4\begin{pmatrix}p_5\\v_5\end{pmatrix}\end{matrix}\right\}\begin{pmatrix}p_1\\v_1\end{pmatrix}=T_1T_2T_3T_4\begin{pmatrix}p_5\\v_5\end{pmatrix}=T_G\begin{pmatrix}p_5\\v_5\end{pmatrix}\end{equation*}$

Pour finir, à partir de cette matrice, les indicateurs acoustiques (coefficient d’absorption et perte par transmission) peuvent être calculés.

3. Méthode des matrices de transfert en parallèle

Figure 2. Schéma d’un empilement parallèle de n matériaux

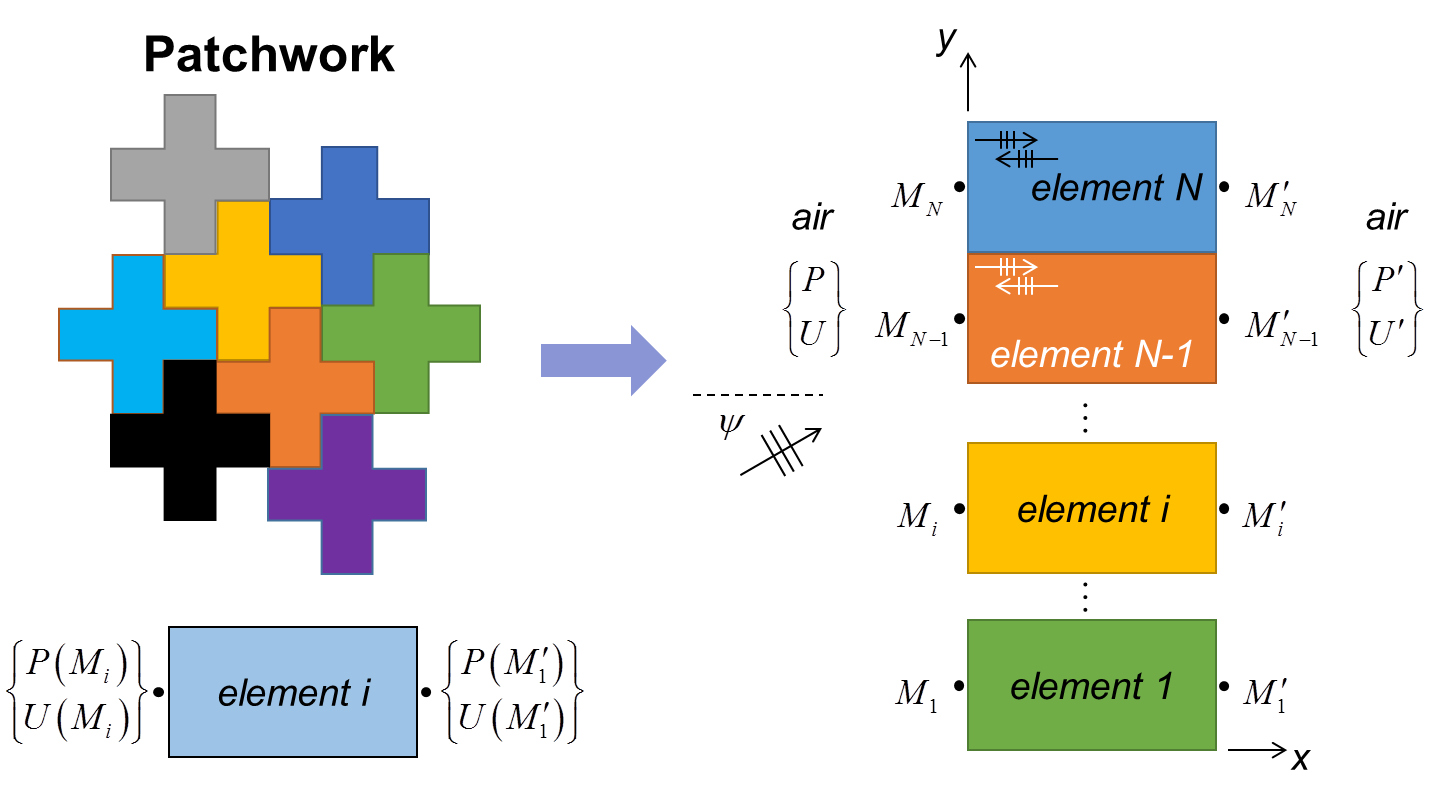
Cette méthode a été publiée récemment . Au lieu d’empiler les couches l’une après l’autre, il est question de trouver la matrice globale d’un empilement de matériaux (ou éléments) l’un à côté de l’autre (parallèle à la direction de propagation du son).

Des hypothèses doivent être posées :

il n’y a que des ondes planes qui se propagent dans l’empilement,
il n’y a que des ondes planes qui se propagent avant et après l’empilement,
il n’y a pas d’échanges entre les éléments constitutifs (pas de diffusion),
la longueur d’onde est grande devant la taille caractéristique de l’empilement,
chaque élément est représenté par une matrice 2 par 2.

Chaque élément est exprimé par sa matrice $T_i$ (Equation 1). Afin de simplifier les calculs, cette matrice est transformé en une autre matrice, appelé matrice d’admittance. L’équation 3 donne l’aperçue de la dite matrice.

(3) $\begin{equation*}\begin{pmatrix}P_i\\U_i\end{pmatrix}=\begin{bmatrix}T_{i,11}&T_{i,12}\\T_{i,21}&T_{i,22}\end{bmatrix}\begin{pmatrix}P_i'\\U_i'\end{pmatrix}\Rightarrow\begin{pmatrix}U_i\\U_i'\end{pmatrix}=\begin{bmatrix}y_{i,11}&y_{i,12}\\y_{i,21}&y_{i,22}\end{bmatrix}\begin{pmatrix}P_i\\P_i'\end{pmatrix}\end{equation*}$

En utilisant la continuité de la pression et des débits de part et d’autre de l’empilement, une matrice globale $T_p$ peut être exprimée. L’équation 4 fournit les infos nécessaires au calcul de cette matrice.

(4) $\begin{equation*}\begin{pmatrix}P\\U\end{pmatrix}=T_p\begin{pmatrix}P'\\U'\end{pmatrix}=\frac{-1}{\sum r_iy_{i,21}}\begin{bmatrix} \sum r_iy_{i,22} & -1 \\ \sum r_iy_{i,22}\sum r_iy_{i,11}-\sum r_iy_{i,12}\sum r_iy_{i,21} & -\sum r_iy_{i,11}\end{bmatrix}\begin{pmatrix}P'\\U'\end{pmatrix}\end{equation*}$

Pour finir, à partir de cette matrice, les indicateurs acoustiques (coefficient d’absorption et perte par transmission) peuvent être calculés. Cette matrice peut être également combinée en série avec d’autre matrice et ainsi créer des construction complexe.

D’autres études ont été publiées :

Utiliser cette méthode à l’envers. Le but est de mesurer l’empilement puis de déterminer les caractéristiques de chaque couche .
Comparer cette méthode avec la méthode de la somme des admittances .
Prendre en compte des phénomènes d’échanges telles que la diffusion (supprimer l’hypothèse 3) .

Méthode des matrices de transfert en parallèle

Table des matières

1. Introduction

2. Méthode des matrices de transfert classique (en série)

3. Méthode des matrices de transfert en parallèle

4. Références